Aby upiec jedno ciasto, Julia potrzebuje 6 jajek, 500g mąki, 300g cukru i 150g masła. Rozgląda się po swojej kuchni i znajduje 2 kostki masła po 250g każda, 2 kg mąki, 1 kg cukru i 3 tuziny jaj (1 tuzin = 12 sztuk). Ile ciast maksymalnie może upiec Julia? (każde ciasto winno zawierać wszystkie składniki w wymaganych ilościach).

Ślimak wspina się po murze. Pierwszego dnia, rano pokonuje 50 cm startując od podstawy muru. Po południu, wyczerpany, opuszcza się o 20 cm i zasypia. W ten sam sposób postępuje każdego następnego dnia. Mur ma wysokość 3,50 m. W którym dniu tej wspinaczki ślimak osiągnie szczyt muru?

Siedem monet odwróconych reszkami do góry ułożono w rzędzie. W każdym ruchu odwraca się trzy dowolnie wybrane monety. Jaką minimalną liczbę ruchów trzeba wykonać, aby wszystkie monety były odwrócone orłami do góry?

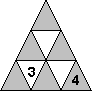
Liczby całkowite od 1 do 9 należy wpisać w dziewięć małych trójkątów tak, by suma liczb znajdujących się w szarych trójkątach była 2 razy większa od sumy liczb z białych trójkątów. Aby ci pomóc, dwie liczby zostały już umieszczone w trójkątach. W karcie odpowiedzi wpisz tylko liczby w białych trójkątach. Jeśli jest więcej niż jedno rozwiązanie, to podaj tylko jedno z nich.

Podczas szkolnej olimpiady sportowej Adam, Bartek, Czarek i Damian zdobyli 21 medali. Bartek zdobył ich najwięcej, ale nie więcej niż 10. Damian ma tych medali dwa razy więcej niż Czarek, Adam zaś o 3 medale więcej niż Damian. Ile medali zdobył Bartek?

Trzeba podzielić przedstawiony na rysunku teren na 4 działki o tej samej powierzchni, mające ten sam kształt i w taki sposób, żeby każda działka zawierała taką samą liczbę drzew (drzewa są oznaczone kropkami). Obrysować, po liniach kratkowania, grubą kreską granice 4 działek.

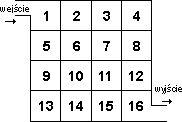
W tym labiryncie dodaje się liczby z pól, przez które się przechodzi. Nie można przechodzić z jednego pola na drugie, jeżeli nie mają one wspólnego boku oraz nie można przechodzić dwa razy przez to samo pole. Jaką największą sumę można osiągnąć przechodząc przez ten labirynt?

Wiadomo, że Tomek ma co najmniej 100 monet, ale nie więcej niż 150. Układa te monety w stosy po 9 monet. Po ułożeniu pewnej liczby stosów zauważył, że liczba pozostałych monet była równa liczbie ułożonych stosów. W przypadku, gdy układał te same monety w stosy po 7 sztuk, również, przy pewnej liczbie stosów, uzyskał ten sam efekt, tj. liczba pozostałych monet była równa liczbie ułożonych stosów. Ile monet miał Tomek?

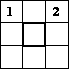
W pola planszy (na rysunku poniżej) należy wpisać liczby całkowite od 3 do 9 (liczby 1 i 2 zostały już umieszczone) w taki sposób, żeby:

• suma czterech liczb umieszczonych w polach kwadratów 2×2 była taka sama
• liczba napisana w polu środkowym (wyróżnionym obwódką) była możliwie największa

Na kongresie w Mathville zebrało się 2000 matematyków, z których kaźdy jest specjalistą tylko w jednej dziedzinie: albo jest arytmetykiem, albo algebraikiem, albo geometrą. Wśród nich są 2 kategorie ludzi: kłamcy, którzy zawsze kłamią oraz prawdomówni, którzy zawsze mówią prawdę. Organizatorzy kongresu zadają kolejno każdemu uczestnikowi trzy pytania: "czy jesteś algebraikiem?", "czy jesteś arytmetykiem?", "czy jesteś geometrą?". Liczby odpowiedzi TAK na każde z pytań są odpowiednio równe: 100, 540, 1610. Ilu jest kłamców na tym kongresie?

Franek pisze ciąg liczb używając tylko cyfr 1, 2, 3, 4 i 5 w taki sposób, że:

• dwie cyfry napisane obok siebie są różne
• wszystkie liczby dwucyfrowe utworzone z dwóch napisanych obok siebie cyfr są różne

Pewnego dnia matematyk de Morgan, który urodził się i zmarł w XIX wieku, na pytanie ile ma lat, odpowiedział w taki sposób: "...miałem y lat w roku, którego numer był równy kwadratowi y...". W którym roku urodził się de Morgan?

Zaczynając od 1 i wykonując tylko dwa działania:

• dodawanie jedynki
• mnożenie przez trzy

Pokratkowana plansza 4×4 została pokryta szesnastoma kartami: 1(as), 2, 3 i 4 każdego z czterech kolorów (trefl, karo, pik i kier). Karty są odwrócone grzbietami. As, 2, 3 i 4 znajduje się w każdym wierszu, w każdej kolumnie i w każdym z czterech mniejszych kwadratów 2×2 (powstałych po narysowaniu linii pomiędzy drugą i trzecia kolumną oraz między drugim i trzecim wierszem). Ponadto, karta trefl, kier, pik i karo znajduje się również w każdym wierszu, w każdej kolumnie i w każdym wyróżnionym kwadracie. Jedynka pik i dwójka kier zostały już odwrócone. Gdzie może być schowana trójka trefl? W karcie odpowiedzi podać liczbę wszystkich możliwych miejsc dla tej karty i współrzędne tych miejsc (dla 1 pik są to współrzędne (1,1), dla 2 kier - (3,4)).

W turnieju szachowym uczestniczyła parzysta liczba graczy. Każdy rozegrał dokładnie jedną partię z każdym z pozostałych. Pięciu graczy przegrało po 2 partie (każdy z nich), a pozostali gracze wygrali po 2 partie (każdy z nich). Nie było żadnego remisu. Ilu graczy uczestniczyło w tym turnieju?

Gdy poprosimy leniwego ucznia Piotra lekceważącego arytmetykę, aby wykonał mnożenie dwóch liczb całkowitych dwucyfrowych, to będziemy zaskoczeni jego metodą postępowania. Otóż wybiera on po jednej cyfrze z każdego czynnika, oblicza iloczyn tych cyfr, a następnie dopisuje (z lewej lub z prawej strony) do niego iloczyn dwóch pozostałych cyfr. Oczywiście, otrzymany przez niego wynik jest prawie zawsze fałszywy. Ale pewnego razu udało mu się, o dziwo(!), otrzymać prawidłowy wynik, który jest liczbą czterocyfrową nie mającą w swoim zapisie cyfry 0. Znaleźć tę liczbę czterocyfrową.

Długość boku kwadratowej parceli wyraża się liczbą całkowitą hektometrów. Pewien punkt wewnętrzny tej parceli znajduje się w całkowito-liczbowych odległościach (w hektometrach) od dwóch nierównoległych boków parceli oraz od wierzchołka wspólnego dla dwóch pozostałych boków. Wiedząc, że suma tych trzech odległości wynosi 10 hm, obliczyć powierzchnię parceli.

Zebrało się 36 członków rodziny Chandelle, wszyscy w różnym wieku. Najmłodszy uczestnik zebrania miał 21 lat, a najstarszy 56 lat. Aby upamiętnić to spotkanie, urządzono sesję zdjęciową. Na każdym zrobionym zdjęciu znajduje się 6 osób i zawsze istnieją wśród nich co najmniej dwie osoby, których lata wyrażają się kolejnymi liczbami. Nie zrobiono dwóch zdjęć z tymi samymi osobami. Ile co najwyżej zrobiono zdjęć?