Odkryj regułę według której powstają kolejne wyrazy ciągu liczbowego 18, 9, 14, 7, 12, 6, 3, 8, , i uzupełnij ten ciąg o kolejne dwa wyrazy.

Sześć liczb: 1, 2, 3, 4, 5 i 6 należy umieścić w kółkach tak, żeby suma liczb w trzech kółkach każdego małego trójkąta była mniejsza lub równa 9.

W butiku "Pod szaloną miotłą" sprzedaje się rekwizyty dla czarowników. Sprzedawczyni - wiedźma handluje 35 godzin w tygodniu. W niedzielę butik jest otwarty od godziny pierwszej w nocy do godziny siódmej rano. W pozostałych dniach tygodnia butik otwierany jest o godzinie dziewiętnastej i zawsze jest zamykany o tej samej godzinie. O której godzinie butik zamykany jest w środę ?

Plansza 5×5 podzielona jest na 25 małych pól kwadratowych. W wybrane 24 pola planszy należy wpisać liczby całkowite od 1 do 6 - każdą z tych liczb czterokrotnie i w taki sposób aby:

• ta sama liczba nie pojawiła się dwukrotnie w żadnej linii poziomej ani w żadnej linii pionowej planszy,
• różnica pomiędzy sumą liczb wpisanych w pola leżące na jednej przekątnej, a sumą liczb wpisanych w pola leżące na drugiej przekątnej była jak największa.

Marek dodał dwie liczby palindromiczne trzycyfrowe i otrzymał w wyniku liczbę palindromiczną czterocyfrową. Do napisania dodawanych liczb i ich sumy użył tylko trzech różnych cyfr, a jednej z nich użył pięciokrotnie. Podaj liczby napisane przez Marka oraz sumę tych liczb.Uwaga: Liczbę palindromiczną czyta się tak samo od strony lewej do prawej i od strony prawej do lewej, np: 44, 101, 9779.

Kiedy miałem 3 lata, mój ojciec był o 5 lat, starszy od mojej mamy. Gdy miałem 9 lat moja mama miała 37 lat. Przed dwoma laty mój ojciec obchodził jubileusz swojego 60-lecia. Ile lat mam teraz ?

W każdym pudełku ustawionym na stole znajduje się co najmniej jeden orzech, ale liczba orzechów w każdym z pudełek jest nie wieksza niż liczba wszystkich pudełek. Liczby orzechów w różnych pudełkach sa różne i w żadnym z pudełek nie ma 13 orzechów. Ile co najwyżej pudełek ustawiono na stole ?

Romek narysował na prostokątnej kartce papieru 3 linie proste p, q, r. Zauważył, że podzieliły one kartkę na 7 części. Dorysował 3 nowe linie proste, jedną równoległą do p, jedną równoległą do q i jedną równoległą do r, w taki sposób, aby trzy nowe linie proste wraz z liniami p, q i r podzieliły kartkę papieru na możliwie najwiekszą liczbę części. Ile było tych części.

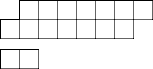
Do tej gry potrzebna jest plansza oraz płytki (rys. przedstawia planszę i jedną płytkę), z których każda pokrywa dokładnie dwa sąsiednie pola planszy leżące w linii poziomej albo w linii pionowej. Każdy gracz w każdym ruchu kładzie jedną taką płytkę na niezajętych jeszcze dwóch sąsiednich polach planszy. Wygrywa ten z graczy, który wykona ostatni dopuszczalny ruch. Dziś grę rozpoczyna Adaś, drugi ruch wykonuje Bartek, a następnie ruchy wykonują na przemian. Czy Adaś ma strategię wygrywającą, tzn. czy wygra zawsze, niezależnie od sposobu gry Bartka ? W Karcie odpowiedzi wpisz NIE albo TAK, ale jeśli wpiszesz TAK, to musisz podać, ile jest różnych ruchów, którymi Adaś może rozpocząć zwycięską grę.

Kasia spędza wolny czas bawiąc się liczbami. Spojrzała na datę 31/12/04 ostatniego dnia bieżącego roku i utworzyła z niej liczbę sześciocyfrową 311204. Potem wyszukiwała liczby całkowite dodatnie mniejsze od 311204, które w swoim zapisie cyfrowym zawierają blok 421 złożony z trzech cyfr 4, 2 i 1 wystepujących w podanej kolejności, jak np. w liczbach: 42154 lub 2142114. Ile jest wszystkich liczb sześciocyfrowych, które mogła wyszukać Kasia ?

W trójkącie prostokątnym ABC o przyprostokątnych CA=12cm i BC=15cm boki zostały podzielone na trzy równe części punktami C₁, C₂, A₁, A₂, B₁, B₂ (rys.). Oblicz pole trójkąta, którego jeden bok ma długość taką jak odcinek CC₁, drugi jak AA₁, a trzeci jak BB₁.

Na płaskim, prostokątnym dachu pewnego budynku pracownik telekomunikacji instaluje maszt w precyzyjnie wybranym miejscu. Maszt został umieszczony w tym miejscu pionowo za pomocą czterech prostoliniowych stalowych prętów biegnących od wierzchołka masztu do czterech rogów prostokątnego dachu. Dwa pręty umocowane do dwóch przeciwległych rogów dachu mają długości 10 i 11 metrów, a dlugość trzeciego pręta jest równa 14 metrów. Jaką długość (w metrach) ma czwarty pręt ?

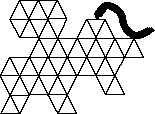
Figura na rysunku przedstawia konia trojańskiego. Należy tę figurę rozciąć na 3 części, z których, bez odwracania na drugą stronę, można złożyć pełny trójkąt równoboczny. Uwaga: Cięcie może przechodzić przez wnętrza małych trójkątów. W Karcie odpowiedzi zaznacz wykonane cięcia i każdą część pokoloruj inaczej.

W grupie złożonej z 16 osób każda osoba ma dokładnie trzech znajomych w tej grupie. Czy zawsze można wszystkie osoby z tej grupy ustawić parami tak, aby w każdej parze znalazły się osoby, które się znają ? Zakładamy, że relacja znajomości jest symetryczna, tzn. że jeśli osoba A zna osobę B, to również B zna A. W Karcie odpowiedzi wpisz TAK lub NIE, ale w przypadku odpowiedzi NIE narysuj graf relacji znajomości w takiej grupie, czyli narysuj 16 punktów reprezentujących osoby wystepujące w grupie i odpowiednie linie łaczące osoby, które się znają.

W siedzibie Klubu Miłośników Gier Logicznych znajduje się zegar, który ma trzy wskazówki. Każda wskazówka może zajmować jedną z 60 pozycji. Wskazówki nie poruszają się w sposób ciągły, lecz przeskakują z jednej pozycji na drugą. O godzinie 12:00:00 wszystkie wskazówki pokrywają się. Wskazówka sekundowa zmienia swoje położenie co sekundę, minutowa co pełną minutę, a godzinowa co pełne 12 minut. Na tarczy zegara jest 60 kresek oznaczających pełne minuty, przy czym co piąta, pogrubiona, oznacza pełne godziny. Zegar jest w remoncie. Z tarczy zdjęto liczby opisujace pełne godziny, a oryginalne wskazówki, na czas remontu, zastapiono trzema jednakowymi. Tarcza zegara zostala też przypadkowo obrócona i nie wiadomo, gdzie jest godzina 12. Jednak zegar caly czas chodzi, a wskazówki poruszają się zgodnie z opisanymi wyżej zasadami. Pewnego popołudnia prezes Klubu spojrzał na zegar i zauważył, że wskazówki zegara utworzyly literę T. Po nie-calych 30 minutach ponownie spojrzał na zegar i spostrzegł, że wskazówki tworzą ze sobą kąty 120° (rysunek poniżej). Która była godzina (z dokładnością do sekundy) w chwili, gdy prezes pierwszy raz spojrzał na zegar ?

Liczby rzeczywiste a, b i c dobrano tak, że dla dowolnych x spelniających warunek -1 ≤ x ≤ 1 mamy nierówność : | ax² + bx + c | ≤ 1. Jaką najwiekszą wartość może osiągnąć wyrażenie | cx² + bx + a | na przedziale [-1,1] ?

Ojciec ma 4 różne bursztynowe sześciany, których długości krawędzi są liczbami całkowitymi centymetrów. Chce on podarować 2 sześciany swojej córce i 2 sześciany synowi. Nie wie jednak jak to zrobić, aby podzial był sprawiedliwy. Na szczęście mama zauważa, ze można dac po 2 sześciany każdemu dziecku w taki sposób, żeby suma objętości sześcianów otrzymanych przez każde z nich byla taka sama. Podać (w cm³) tę wspólną sumę wiedząc, że chodzi o rozwiązanie możliwie najmniejsze.

Los pewnej loterii sprzedawany w cenie 10 euro jest zdrapką o 36 polach ułożonych w kwadrat 6 × 6. Wiadomo, że 6 pól zawiera liczbę "10", 9 pól zawiera liczbę "1", a każde z pozostałych 21 pól zawiera liczbę "0". Gracz może zdrapywać pola według własnego uznania, tyle, ile zechce, ujawniając zawarte w nich liczby. Kiedy postanawia przerwać zdrapywanie, mnoży liczby, które odkrył (uwzgledniając zera) i wygrywa tyle euro, ile wynosi otrzymany iloczyn. Zakłada się, że wszyscy gracze, którzy kupili los stosują strategię optymalną. Statystycznie, jaki procent pieniędzy wydanych na zakup losów zostanie zwrócony graczom ? Wynik zaokrąglić do najbliższej jednej dziesiątej procenta.