Kod jest liczbą trzycyfrową, w której suma cyfr jest równa 15, a cyfra jedności jest trzykrotnie większa od cyfry setek. Podaj dwa takie kody trzycyfrowe.

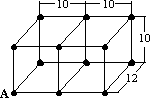
Na rysunku poniżej pokazana jest siatka przestrzenna przedstawiająca prostopadłościan o wymiarach: 20 cm, 12 cm, 10 cm, który powstał z połączenia dwóch mniejszych prostopadłościanów. Mrówka znajduje się w węźle A i chce odwiedzić wszystkie 11 z pozostałych węzłów, a następnie powrócić do węzła A. Cały ten spacer chce odbyć po możliwie najkrótszej drodze. Podaj w centymetrach długość drogi, po której odbędzie ten spacer.

Myszki A, B, C, D i E biorą udział w rewii i w przerwie występów porównują wielkości swoich kokardek. Kokardka myszki A jest większa niż kokardka myszki B. Kokardka myszki B jest mniejsza od kokardek myszek C i D. Myszka E ma kokardkę większą niż myszka D i mniejszą niż myszka C. Zauważyły też, że kokardka myszki C nie jest największa. Ustawić te 5 myszek od lewej do prawej według wielkości ich kokardek i tak, by pierwsza z lewej miała kokardkę najmniejszą.

Marek zauważył, że liczby 279 i 280 są kolejnymi liczbami naturalnymi o takiej własności, że mniejsza ma sumę cyfr podzielną przez 6, a większa ma sumę cyfr podzielną przez 5. Znajdź mniejsze, również kolejne liczby naturalne o tej samej własności.

Na niektórych polach planszy 6 × 6 ustawiono po jednym pionku, a pozostałe pola tej planszy są puste. Agnieszka pozliczyła pionki ustawione na polach kolejnych linii poziomych planszy i otrzymała 6 różnych liczb całkowitych. Bartek zlicza pionki ustawione na polach kolejnych linii pionowych planszy i stwierdza ze zdumieniem, że żadna z otrzymanych przez niego liczb nie występuje wśród liczb otrzymanych przez Agnieszkę. Podaj, w kolejności rosnącej, sześć liczb otrzymanych przez Agnieszkę.

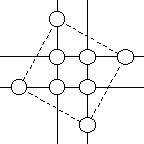
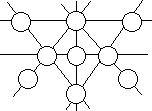
Osiem kółek rozmieszczono na czterech różnych liniach prostych tak, że na każdej z nich znalazły się trzy kółka. W kółka te należy wpisać liczby 1, 2, 3, 4, 5, 6, 7 i 8 w taki sposób, aby suma trzech liczb wpisanych w kółka leżące na tej samej linii prostej była zawsze taka sama, a suma liczb wpisanych w cztery kółka tworzące wewnętrzny kwadrat była dwukrotnie większa od sumy liczb wpisanych w cztery kółka tworzące zewnętrzny kwadrat. Podać, w kolejności rosnącej, liczby wpisane w kółka tworzące wewnętrzny kwadrat.

W trakcie meczu piłki ręcznej pomiędzy drużynami A i B, który zakończył się wynikiem 23:19 (na korzyść drużyny A) miał miejsce taki moment, w którym drużyna A miała tyle zdobytych bramek, ile bramek zdobyła drużyna B w pozostałej, do końca, części meczu. Podać, ile w tym momencie miały zdobytych bramek łącznie obie drużyny.

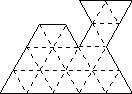
Podzielić figurę, pokazaną na rysunku poniżej, na trzy jednakowe części dające się nałożyć jedna na drugą przez przesuwanie i obracanie, ale bez odwracania na drugą stronę. Linie podziału zaznaczyć starannie pogrubionymi kreskami w karcie odpowiedzi.

Liczby 2, 4, 6, 8, 10, 12, 14, 16, 18 i 20 rozdzielamy na dwie grupy L (licznik) i M (mianownik) po 5 liczb w każdej grupie tak, aby wynik dzielenia iloczynu liczb występujących w grupie L przez iloczyn liczb występujących w grupie M był liczbą całkowitą najmniejszą z możliwych. Podaj, w kolejności rosnącej, 5 liczb które umieściłeś /-aś/ w grupie L.

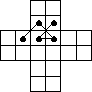
Król szachowy odbywa spacer po polach planszy (pokazanej na rys. poniżej) według reguł gry w szachy. Wystartował ze środka pewnego pola i powrócił na to samo pole, a na każdym innym polu był dokładnie jeden raz. Porusza się zawsze ze środka pola do środka następnego pola po odcinkach łączących te środki. Jego droga jest łamaną składającą się tylko z dwóch rodzajów odcinków, krótszych i dłuższych, łączących środki dwóch pól mających albo wspólny bok, albo tylko wspólny wierzchołek. Na rysunku pokazany jest fragment możliwej łamanej złożony z czterech odcinków. Ile dłuższych odcinków znajdzie się w najdłuższej drodze króla?

Jasio, ze zbioru 13 liczb naturalnych 1, 2, 3, ... , 13 usunął jedną liczbę, a pozostałe ustawił w 6 par. Obliczył sumę liczb w każdej parze i ze zdziwieniem zauważył, że otrzymał 6 kolejnych liczb naturalnych. Z kolei Joasia skreśliła również jedną, inną liczbę naturalną spośród liczb 1, 2, 3, ... , 13 i, postępując dalej podobnie jak Jasio, otrzymała 6 kolejnych liczb naturalnych, których suma była jednak większa od sumy sześciu kolejnych liczb naturalnych Jasia. W rozwiązaniu Joasi, w jednej parze znalazły się liczby 6 i 9. W karcie odpowiedzi podaj wszystkie pary utworzone przez Joasię łącznie z parą (6,9) w takiej kolejności, aby sumy liczb w kolejnych parach tworzyły ciąg rosnący. Uwaga: w każdej parze na pierwszym miejscu wypisać liczbę mniejszą.

Z przedziału domkniętego [0,2] wybieramy pięć liczb x₁, x₂, x₃, x₄, x₅ i obliczamy iloczyn

W = (x₁ - x₂)(x₂ - x₃)(x₃ - x₄)(x₄ - x₅)(x₅ - x₁)

Jaki największy wynik możemy otrzymać? W karcie odpowiedzi podać maksymalną wartość W oraz liczby x₁, x₂, x₃, x₄, x₅, dla których ta maksymalna wartość jest osiągnięta.

Liczbę 6 możemy przedstawić w postaci sumy trzech różnych składników 1, 2 i 3 (6=1+2+3), które mają taką własność, że suma dowolnych dwóch jest podzielna bez reszty przez ich różnicę. Np. 3 + 1 = 4 dzieli się przez 3 - 1 = 2. Przedstawić liczbę 45 w postaci sumy x₁+ x₂ + x₃ + x₄ + x₅ pięciu różnych składników naturalnych tak, aby suma x_i + x_j dowolnych dwóch z tych składników, i ≠j, dzieliła się bez reszty przez różnicę x_i - x_j.

W kółka diagramu należy wpisać liczby naturalne od 1 do 9 tak, aby suma trzech liczb wpisanych w kółka leżące na tej samej linii prostej była zawsze taka sama. Podać dwa rozwiązania, w których sumy trzech liczb wpisanych w kółka leżące na górnej, poziomej linii prostej są różne.

W trójkącie ostrokątnym ABC dany jest promień koła opisanego R = 12 cm i promień koła wpisanego r = 8 cm. W trójkącie tym rysujemy trzy koła o takim samym promieniu ρ, z których każde jest styczne do ramion innego kąta tego trójkąta i które nie mają wspólnego punktu wewnętrznego. Jaką największą wartość może mieć ρ?

Zadanie to unieważniono, ze względu na złe dane. (Iloraz R/r nie może być mniejszy niż 2). Rozwiązać to zadanie przy R = 14 cm, r = 6 cm.

W liczbie pięciocyfrowej jedna z cyfr jest zerem. Jeżeli usuniemy tę cyfrę i nie zmieniając porządku pozostałych cyfr utworzymy liczbę czterocyfrową, to iloczyn tej liczby przez 9 daje w wyniku wyjściową liczbę. Podać wszystkie liczby pięciocyfrowe o takiej własności.

Funkcja f(x) = ax² + bx + c spełnia warunki:

|f(-1)| ≤ 1, |f(0)| ≤ 1 i |f(1)| ≤ 1

Jaką największą wartość funkcja ta może osiągnąć na przedziale <0,1>?

Wielościan wypukły W spełnia dwa następujące warunki:

• 1. Każdy czworościan zawarty w W ma objętość ≤ 1 dm³.
• 2. Dla każdego punktu Q leżącego na zewnątrz W można znaleźć trzy punkty P₁, P₂, P₃ należące do wielościanu W takie, że czworościan P₁P₂P₃Q ma objętość > 1 dm³,