1 - Kuba pisze, w pewnej kolejności, liczby całkowite według własnego systemu,
a Agata odgaduje jaki jest ten system. Gdy Kuba napisał dziesięć pierwszych liczb
1, 1, 2, 3, 3, 7, 4, 15, 5, 31, ...
to Agata powiedziała z uśmiechem - "Już znam twój system" - i szybko napisała następne dziesięć
liczb ciągu Kuby. Podaj dwie ostatnie liczby napisane przez Agatę. | 
2 - Ania, Beata, Ewa, Ola i Sylwia wybierają się autobusem na wycieczkę i
utworzyły kolejkę przed pustą kasą biletową. Ola stała bliżej kasy niż Beata, ale w tej
kolejce znalazła się za Sylwią. Ania i Sylwia nie stały obok siebie. Ewa nie stała obok
Sylwii, ani obok Oli, ani obok Ani. W jakiej kolejności dziewczynki te ustawiły
się przed kasą biletową ? W Karcie Odpowiedzi wpisać tylko pierwsze litery imion
dziewczynek. | 
3 - Na wystawie sklepu z zabawkami ustawiono rząd pluszowych przytulanek.
Były tam misie, pięć kotków i dwa hipopotamy. Każdy kotek w tym rządzie przytulał się do
dwóch misiów, a każdy miś miał z jednej strony kotka, a z drugiej strony albo misia albo
hipopotama. Ile było misiów w tym rzędzie przytulanek ? | 
4 - Beata napisała 10 kolejnych liczb całkowitych dodatnich, z których każda
miała sumę cyfr niepodzielną przez 7. Najmniejsza z tych dziesięciu liczb była liczbą dwucyfrową.
Jaka to była liczba ? | 
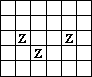
5 - Na białym papierze rysujemy prostokąt i dzielimy go na 30 jednakowych
pól kwadratowych. Trzy pola, wskazane na rysunku poniżej, malujemy na kolor zielony Z, a
niektóre białe pola malujemy na kolor czarny C. Pola do zamalowania na czarno wybieramy tak,
aby każde pole białe i każde pole zielone, a także każde pole czarne miało co najmniej
jednego sąsiada koloru czarnego. Przyjmujemy, że dwa pola sąsiadują, gdy mają wspólny bok.
Jaką najmniejszą liczbę białych pól trzeba pomalować na czarno, aby spełnione były
wyżej podane warunki ? W Karcie Odpowiedzi należy podać tę liczbę oraz trzy różne
przykłady rozmieszczenia czarnych pól C.
| 
6 - W klasie Tomka grzecznych dzieci jest trzykrotnie więcej niż niegrzecznych.
Natomiast grupa złożona z grzecznych dziewczynek i niegrzecznych chłopców jest dwukrotnie
liczniejsza od grupy złożonej z grzecznych chłopców i niegrzecznych dziewczynek. Wszystkich
chłopców w tej klasie jest tylu ile jest grzecznych dziewczynek. Ilu chłopców jest w
tej klasie, jeżeli wiadomo, że klasa ta liczy nie więcej niż 40 uczniów ? | 
7 - Nauczyciel polecił Jankowi, aby z cyfr 1, 2, 3, 4, 5, 6, 7, 8 i 9 utworzył
trzy liczby trzycyfrowe wykorzystując każdą z podanych cyfr dokładnie jeden raz. Janek napisał
trzy takie liczby, a następnie obliczył ich sumę, która okazała się liczbą palindromiczną.
Jaka to była liczba palindromiczna ? Liczba jest palindromem, jeżeli napisana
jest układem symetrycznym cyfr, jak np. liczby: 121, 2002, 3773, 12021. | 
8 - Jednoosobowa gra koniem szachowym odbywa się na planszy kwadratowej
11 × 11 podzielonej na 121 pól kwadratowych. W tej grze ruchy wykonuje się jednym
koniem szachowym, tak jak w grze w szachy. W grze obowiązują następujące reguły:
- 1° W trakcie gry koń nie może znaleźć się dwukrotnie na tym samym polu planszy
i nie może powrócić na pole, z którego rozpoczynała się gra,
- 2° Gry nie wolno przerwać, jeżeli możliwy jest jeszcze do wykonania następny ruch.
Druga reguła oznacza, że gra kończy się tylko wtedy, gdy nie może być kontynuowana
zgodnie z pierwszą regułą. Mistrzem w tej grze zostaje ten, kto startując z dowolnie
wybranej pozycji początkowej, potrafi zawsze zakończyć grę minimalną liczbą ruchów.
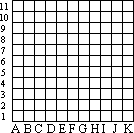
Po ilu ruchach mistrz zakończy grę, jeżeli rozpocznie ją koniem ustawionym
na polu A11, tzn. na lewym górnym polu planszy ? W Karcie Odpowiedzi podać
liczbę ruchów wykonanych przez mistrza i oznaczyć te pola, na których może on zakończyć
grę używając symboli, np. G7, A3, K10.
| 
9 - Do ścisłego finału konkursu matematycznego Jury zakwalifikowało 3
uczniów. Każdy z nich otrzymał taki sam zestaw 16 zadań. Regulamin konkursu ustala, że
za prawidłowe rozwiązanie każdego z tych zadań uczeń otrzymuje 8 punktów, za nietknięte
lub tylko częściowo rozwiązane zadanie otrzymuje 0 punktów, a za każde błędnie
rozwiązane zadanie uczeń otrzymuje 5 punktów karnych, które odejmuje się od sumy punktów
uzyskanych za prawidłowo rozwiązane zadania. Każdy z uczestników finału miał taką samą
liczbę błędnie rozwiązanych zadań, ale każdy z nich miał inną liczbę zadań rozwiązanych
prawidłowo. Po odjęciu punktów karnych cała trójka miała łącznie 149 punktów. Ile
zadań każdy z nich rozwiązał prawidłowo? Jeżeli możliwe są różne odpowiedzi, to
należy podać wszystkie pisząc liczby w kolejności malejącej. | |

10 - Kwadrat o boku 10 cm podzielono linią prostą na dwie figury w taki sposób,
że obwody otrzymanych figur różniły się o 8 cm, a dodatnia różnica pól tych figur była
najmniejsza z możliwych. O ile centymetrów kwadratowych różniły się pola tych dwóch
figur? | 
11 - Znale siedem kolejnych liczb naturalnych nieparzystych, ktrych suma
jest szecianem liczby pierwszej. W Karcie Odpowiedzi poda te liczby w kolejnoci rosncej. | 
12 - Ze zbioru złożonego ze wszystkich liczb naturalnych od 1 do 100
wybrano możliwie najliczniejszy podzbiór tak, aby suma żadnych dwóch liczb tego podzbioru
nie dzieliła się przez ich różnicę. Ile liczb było w tym podzbiorze? | 
13 - Dwa papierowe kwadraty o polach 9 cm2 i 4 cm2 należy
podzielić na możliwie najmniejszą liczbę wielokątów tak, aby można było złożyć z nich kwadrat
o polu 13 cm2. W Karcie Odpowiedzi narysować dokładnie linie podziału obu kwadratów
zaznaczając liczbowo długości tych boków otrzymanych wielokątów, które leżą na bokach dzielonych
kwadratów. | 
14 - Liczbę  rozkładamy na
sumę sześciu ułamków rozkładamy na
sumę sześciu ułamków
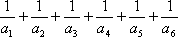
o mianownikach naturalnych parami różnych i spośród wszystkich takich rozkładów wybieramy ten,
w którym suma mianowników jest najmniejsza. Podać, w kolejności rosnącej, mianowniki
wybranego rozkładu.
| 
15 - Znaleźć najmniejszą wartość wyrażenia
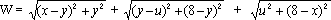
gdzie x, y, u są liczbami rzeczywistymi. W Karcie Odpowiedzi podać też liczby x, y oraz u,
dla których W osiąga najmniejszą wartość. | 
16 - Mówimy, że czworokąt jest wpisany w krzywą Γ, jeżeli wszystkie
wierzchołki tego czworokąta leżą na krzywej Γ. Ile kwadratów można wpisać w
krzywą zamkniętą Γ złożoną z dwóch łuków okręgów o promieniu R = 1 m oraz odcinka AB
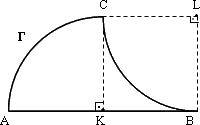
o długości 2 m? Na rysunku poniżej pokazana jest krzywa Γ w zmniejszonej
skali;
| AK | = | KB | = | KC | = | BL | = R.
W Karcie Odpowiedzi podać liczbę wpisanych kwadratów oraz długości boków tych kwadratów.
Wyniki podać w milimetrach zaokrąglone do milimetra.
| 
17 - Znaleźć największą liczbę M taką, że nierówność
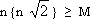
jest prawdziwa dla każdej liczby naturalnej n.
{x} = x - [x] oznacza część ułamkową liczby x. | 
18 - Obliczyć promień największego okręgu leżącego na powierzchni
x2 + 4y2 + 16z2 = 16
| |