Zadanie 1
1 - Odwiedziny koleżanek (współczynnik 1)
Agnieszka, Celina i Dominika mieszkają w tym samym pionie budynku, który ma 5 kondygnacji (tzn. parter i cztery piętra). Dominika chcąc odwiedzić Agnieszkę musi wejść, po schodach, dwa piętra, a jeśli chce odwiedzić Celinę, to schodzi w dół. Na którym piętrze mieszka Dominika, jeżeli wiadomo, że Celina nie mieszka na parterze?
| Zadanie 2
2 - Kwadraty (współczynnik 2)
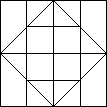
Ile jest wszystkich kwadratów, których boki leżą na liniach narysowanej poniżej figury?
| Zadanie 3
3 - Labirynt (współczynnik 3)
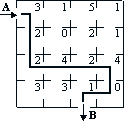
Przy prawidłowym przejściu przez labirynt od wejścia A do wyjścia B, Tomek nie może dwukrotnie znaleźć się w tej samej sali. Za prawidłowe przejście przez labirynt otrzymuje on tyle samo cukierków ile wynosi suma numerów odwiedzanych sal. Zaznacz w Karcie odpowiedzi trzy prawidłowe przejścia, z których każde nagrodzone będzie 13 cukierkami. Uwaga: na rysunku zaznaczono prawidłowe przejście nagrodzone 18 cukierkami.
| Zadanie 4
4 - Pożyczka (współczynnik 4)
Marek mówi do Jarka:
- Pożycz mi 96 groszy.
- Nie mam tyle - odpowiada Jarek.
- A ile masz ? - pyta dalej Marek.
- Odpowiem ci w zagadkowy sposób - mówi Jarek: "Gdybym miał dwa razy tyle groszy ile mam teraz, to po wręczeniu tobie kwoty, o którą prosisz, pozostałoby mi dokładnie tyle, ile teraz brakuje mi, aby spełnić twoją prośbę".
Ile groszy ma Jarek?
| Zadanie 5
5 - Dziurawy prostokąt (współczynnik 5)
Papierowy prostokąt z wyciętymi dwoma otworami należy podzielić na możliwie najmniejszą liczbę części tak, aby można było z tych części zbudować kwadrat. Otrzymane z podziału części można przesuwać po płaszczyźnie i obracać, ale nie można ich odwracać na drugą stronę. Podać dwa różne podziały o minimalnej liczbie części, zaznaczając linie podziału na rysunkach w Karcie odpowiedzi. Przyjmujemy, że dwa podziały są różne, jeżeli przynajmniej jedna z części występująca w jednym podziale nie występuje w drugim. Uwaga: Prostokąt należy ciąć wzdłuż wskazanych, na rysunku, linii przerywanych.
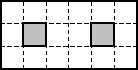
| Zadanie 6
6 - Podział czekolad (współczynnik 6)
Grupa złożona z 6 chłopców otrzymała do podziału 7 jednakowych 150 gramowych tabliczek czekolady. Przy podziale tym muszą być spełnione 3 warunki:
- 1. Porcje przeznaczone dla każdego z chłopców muszą być tej samej wagi.
- 2. Chłopcy mogą rozłamać tabliczkę czekolady, ale tylko na dwie części.
- 3. Liczba rozłamanych czekolad musi być możliwie najmniejsza.
Jak sprytni chłopcy uporali się z tym problemem? W karcie odpowiedzi podać, ile tabliczek chłopcy rozłamali, a ponadto każdą rozłamaną czekoladę podzielić pionową kreską i wpisać wagi, w gramach, powstałych części. Prostokąty przedstawiające nierozłamane czekolady pozostawić puste.
| Zadanie 7
7 - Finał konkursu (współczynnik 7)
W finale konkursu matematycznego, jedno z zadań miało następującą treść: "W kratki taśmy wpisać, w porządku rosnącym, 13 różnych liczb całkowitych dodatnich, których suma wynosi 94". Każdy finalista znalazł rozwiązanie spełniające warunek zadania, ale każdy podał inny wynik. Ilu uczniów - co najwyżej - brało udział w tym finale? Podaj jedno z możliwych rozwiązań tego zadania.

| Zadanie 8
8 - Odważnik (współczynnik 8)
Mamy zestaw złożony z 7 odważników, których wagi, wyrażone w gramach, są liczbami całkowitymi. Wiadomo, że wśród tych odważników jest co najmniej jeden o wadze 1 g oraz co najmniej jeden o wadze 13 g. Wiadomo też, że jeśli z tego zestawu usuniemy jeden z odważników, wybrany dowolnie, to pozostałe 6 odważników można zawsze podzielić na dwie grupy równoważące się na wadze szalkowej. Jaka może być minimalna waga takiego zestawu odważników? Podać też przykład zestawu odważników, którego łączna waga jest minimalna.
| Zadanie 9
9 - Układanka z zapałek (współczynnik 9)
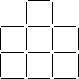
Z 20 zapałek zbudowano układankę zawierającą 7 kwadratów, z których każdy ma brzeg utworzony z 4 zapałek (patrz rysunek). Jaką najmniejszą liczbę zapałek trzeba przełożyć na inne miejsca, aby z tych samych 20 zapałek powstała nowa układanka złożona z 5 kwadratów, takich samych jak w poprzedniej układance? Na podanej figurze, w karcie odpowiedzi, narysować pogrubionymi liniami zapałki pozostawione na swoich miejscach oraz dorysować zapałki przełożone na inne miejsca. Każdą zapałkę przedstawić odcinkiem.
| |
Zadanie 10
10 - Tajemnicza liczba (współczynnik 10)
Znaleźć najmniejszą liczbę całkowitą dodatnią n, która powiększona o iloczyn swoich cyfr daje liczbę większą od n, napisaną za pomocą tych samych cyfr co liczba n, ale nie w tej samej kolejności.
| Zadanie 11
11 - Zagadkowa ósemka (współczynnik 11)
W kratki taśmy należy wpisać osiem różnych liczb całkowitych dodatnich tak, aby suma każdych dwóch liczb sąsiadujących była liczbą parzystą, suma każdych trzech liczb następujących po sobie była podzielna przez 3, suma każdych czterech liczb następujących po sobie była podzielna przez 4, itd., ... , i wreszcie, suma wszystkich ośmiu liczb była podzielna przez 8, a ponadto tak, by suma tych 8 liczb była najmniejszą z możliwych.

| Zadanie 12
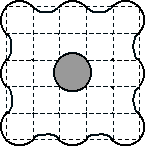
12 - Podział posiadłości (współczynnik 12)
Na rysunku poniżej pokazany jest plan posiadłości z centralnie umieszczonym stawem. Tę część posiadłości, która nie obejmuje stawu, należy podzielić na 6 części w taki sposób, aby każda z nich dała się nałożyć na każdą inną za pomocą przesuwania lub obracania, ale bez odwracania na drugą stronę. Linie podziału zaznaczyć na rysunku w karcie odpowiedzi.
| Zadanie 13
13 - Trójkąt i koła (współczynnik 13)
W trójkącie prostokątnym promień koła wpisanego r = 5 cm, a odległość pomiędzy środkami kół, wpisanego w ten trójkąt i opisanego na tym trójkącie d = 12 cm. Obliczyć obwód i pole tego trójkąta.
| Zadanie 14
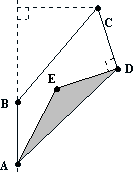
14 - U pana Karpiowskiego (współczynnik 14)
Gospodarstwo pana Karpiowskiego jest czworokątem ABCD (rys. poniżej), w którym część trójkątna AED jest sztucznym stawem rybnym. Bok AB tego gospodarstwa ma długość 240 m, wierzchołek C jest odległy od prostej przechodzącej przez wierzchołki A i B o 320 m, wewnętrzny kąt ABC jest rozwarty. Punkty B, E i D leżą na jednej prostej i współliniowe są także punkty A, E i C. Odcinki ED DC są równe i tworzą kąt prosty, a trójkątny staw ma powierzchnię 31680 m2. Jaką powierzchnię ma pozostała część gospodarstwa pana Karpiowskiego? Podać wynik dokładny w m2.
| Zadanie 15
15 - Suma ułamków (współczynnik 15)
Niech d(n) oznacza liczbę naturalną leżącą na osi liczbowej najbliżej liczby √n, n = 1, 2, ... . Obliczyć sumę
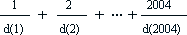
| Zadanie 16
16 - Kryptarytm (współczynnik 16)
W kryptarytmie
NINE × THREE = NEUF × TROIS
zaszyfrowane są dwie liczby naturalne czterocyfrowe i dwie pięciocyfrowe zapisane w układzie dziesiątkowym. Słowa NINE i TROIS przedstawiają liczby podzielne przez 3, a słowa THREE i NEUF przedstawiają liczby podzielne przez 9. Różne litery zastępują różne cyfry, a różne cyfry zostały zastąpione przez różne litery. Znaleźć liczby NINE i THREE oraz ich iloczyn.
| Zadanie 17
17 - Mini-max (współczynnik 17)
Liczbę 1 przedstawiamy jako sumę x1 + x2 + x3 + x4 czterech dodatnich składników x1, x2, x3, x4, a następnie dla każdego takiego przedstawienia wybieramy największą z czterech liczb
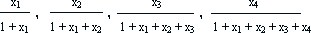
i tak wybraną liczbę oznaczamy przez S(x1, x2, x3, x4). Znaleźć min S(x1, x2, x3, x4) i podać wartości liczb x1, x2, x3 i x4realizujących to minimum.
| Zadanie 18
18 - Potęgowa parzystość (współczynnik 18)
Wyznaczyć wszystkie liczby naturalne n, dla których 31n - 1 dzieli się bez reszty przez 2n.
| |