Zadanie 1
1 - Żabka siedzi na jednym z nenufarów (patrz rysunek) i kolejnymi skokami
z nenufaru na nenufar sąsiedni zamierza osiągnąć nenufar z kwiatem. Może wykonywać skoki
tylko wzdłuż linii pionowych lub wzdłuż linii poziomych. Wykonuje skok ↑ lub ↓,
jeśli po tym skoku chce znaleźć się na nenufarze o numerze parzystym, albo wykonuje skok
← lub → , jeśli po tym skoku chce znaleźć się na nenufarze o numerze nieparzystym.
Zaznacz strzałkami najkrótszą drogę żabki, po której dotrze ona do nenufaru z
kwiatem (na rysunku nenufar ten jest jednocześnie oznaczony liczbą 100).

| Zadanie 2
2 - Z czterech zegarów oznaczonych literami A, B, C i D
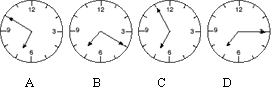
jeden wskazuje dokładny czas, jeden przyśpieszył o 20 minut, jeden opóźnił się o 5 minut,
a jeden przyspieszył o 25 minut. W Karcie Odpowiedzi wpisz literę zegara, który
wskazuje dokładny czas. | Zadanie 3
3 - Dwa jednakowe akwaria napełnione wodą do pełna ważą razem 72 kilogramy,
a jedno takie akwarium napełnione wodą do połowy waży 20 kilogramów. Ile kilogramów
waży jedno puste akwarium ? | Zadanie 4
4 - Liczba 145541 jest palindromem, ponieważ czyta się ją tak samo z lewa na
prawo jak i z prawa na lewo. Ponadto ma ona pewną szczególną własność - wybrane z niej kolejne
liczby dwucyfrowe 14, 45, 55, 54 i 41 są wszystkie różne. Znaleźć największą liczbę
będącą palindromem, w której występują tylko trzy cyfry 1, 2, 3 i która ma również tę szczególną
własność. | Zadanie 5
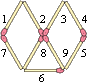
5 - W układance utworzonej z 9 jednakowych zapałek znajdują się różne figury
geometryczne. Są tam m.in. trójkąt {6,8,9}, 2 romby {1,2,8,7} i {3,4,5,9}, a także 2 trapezy
{4,5,6,8,3} i {1,2,9,6,7}. Jak przestawić trzy zapałki, aby otrzymać nową układankę,
w której znajdzie się m. in. 5 trójkątów? Na rysunku, w Karcie Odpowiedzi, można
zapałki zastąpić odcinkami i nie trzeba oznaczać ich cyframi.
| Zadanie 6
6 - W kratki taśmy należy wpisać 11 liczb całkowitych nieujemnych, niekoniecznie
różnych, ale tak dobranych, aby suma liczb wpisanych w jakiekolwiek trzy kolejne kratki taśmy była
zawsze liczbą parzystą, a suma wszystkich jedenastu liczb wpisanych w kratki taśmy była liczbą
nieparzystą i najmniejszą z możliwych. W Karcie Odpowiedzi podaj szóstą z tych liczb oraz sumę
wszystkich 11 liczb.

| Zadanie 7
7 - W rachunku małego Jasia, wykonanym na siedmiu siódemkach, zostały usunięte
znaki dodawania + , znaki mnożenia × , a także nawiasy ( ). Wstaw je ponownie na
właściwych miejscach, aby następująca równość
7 7 7 7 7 7 7 = 707
była prawdziwa. | Zadanie 8
8 - W grupie 5 dziewcząt niektóre są przyjaciółkami, a inne nie. Każda z
dziewcząt ma w tej grupie albo 2 przyjaciółki albo 3 przyjaciółki, a gdy 2 dziewczynki
przyjaźnią się, to nie mają nigdy tej samej liczby przyjaciółek w tej grupie. Ela ma w
tej grupie 3 przyjaciółki. Amelia przyjaźni się z Kasią. Beata jest również przyjaciółką
Kasi. Podaj, w kolejności alfabetycznej, imiona przyjaciółek Dominiki. | Zadanie 9
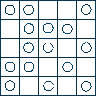
9 - Na polach planszy 5 × 5 ustawiono 15 pionków. Jaką najmniejszą
liczbę pionków trzeba przestawić na inne wolne pola planszy, aby po tej operacji na każdej
linii poziomej i na każdej linii pionowej, a także na każdej z dwóch przekątnych planszy
znajdowały się 3 pionki. W Karcie Odpowiedzi podać liczbę przestawionych pionków,
zaczernić przestawiane pionki i strzałkami zaznaczyć ich ruchy na nowe pozycje.
| |
Zadanie 10
10 - Na płaszczyźnie narysowano cztery okręgi o takim samym promieniu.
Żadne dwa z tych okręgów nie były styczne, a wszystkie cztery okręgi utworzyły figurę
spójną, co oznacza, że z dowolnego punktu tej figury można przemieścić się do każdego
innego punktu tej figury poruszając się po łukach okręgów tworzących tę figurę.
Jaka może być najmniejsza liczba punktów, w których przecinają się co najmniej
dwa z czterech narysowanych okręgów? Uwaga. Rozważaną figurę tworzą same okręgi,
a nie koła.
| Zadanie 11
11 - Marek i Radek podzielili między siebie całą zawartość torby z cukierkami.
Liczba cukierków Marka była liczbą parzystą, zaś Radka liczbą nieparzystą. Iloczyn piątej
części liczby cukierków Marka i czwartej części liczby cukierków Radka był równy sumie
czwartej części liczby cukierków Marka i piątej części liczby cukierków Radka.
Ile cukierków było w tej torbie przed podziałem? | Zadanie 12
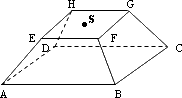
12 - Na stole leży tekturowe, zamknięte pudełko, w którym podstawa ABCD
jest kwadratem o boku równym 12 cm, górna ściana EFGH jest równoległa do podstawy i też
jest kwadratem, ale o boku równym 6 cm. Każda z krawędzi bocznych ma długość 6 cm. W
środek S górnej ściany pudełka wbijamy ostrze cyrkla, a drugie ramię cyrkla ustawiamy
tak, aby grafit znalazł się w wierzchołku E tej ściany. Cyrklem o takiej rozwartości
kreślimy krzywą zamkniętą utworzoną z czterech łuków leżących na ścianach bocznych
pudełka. Podać, w centymatrach, długość tej krzywej. Należy podać
dokładny wynik.
| Zadanie 13
13 - Z cyfr 1 i 2 tworzymy ciąg liczb całkowitych L1, L2,
L3, ... w taki sposób, że L1 = 2, L2 = 1, L3 = 12,
L4 = 121, L5 = 12112, a każda następna liczba w tym ciągu powstaje z dwóch
poprzednich przez dopisanie z prawej strony do ostatniej napisanej liczby, liczbę przedostatnią,
tzn. Ln+1 = Ln Ln-1. Tak więc L6 = L5
L4 = 12112121. Podać symbole trzech najmniejszych liczb podzielnych przez 11
w ciągu L1, L2, ... , wypisując je w kolejności rosnącej. Uwaga:
Przyjmujemy, że liczby tego ciągu napisane są w dziesiątkowym układzie pozycyjnym. | Zadanie 14
14 - Znaleźć najmniejszą wartość wyrażenia

gdzie x i y są liczbami rzeczywistymi. W Karcie Odpowiedzi podać dokładną wartość min W oraz
liczby x i y, dla których W osiąga najmniejszą wartość. | Zadanie 15
15 - Kuba zbudował z cyfr 1, 2, 3, 4, 5, 6, 7 i 8 wszystkie liczby ośmiocyfrowe
C1 C2 ... C8, w których każda z wymienionych cyfr występowała
dokładnie jeden raz i każda cyfra, począwszy od trzeciej, była większa od mniejszej z dwóch cyfr
bezpośrednio ją poprzedzających, tzn. Ck > min {Ck-1, Ck-2} dla
k ≥ 3. Następnie liczby te ustawił w ciąg rosnący. Jaka liczba będzie na 17 miejscu
w tym ciągu? | Zadanie 16
16 - W przestrzeni poprowadzono 6 płaszczyzn. Pięć płaszczyzn przechodziło
przez punkt O i żadne trzy z tych pięciu płaszczyzn nie przecinały się wzdłuż tej samej
prostej. Szósta płaszczyzna nie przechodziła przez punkt O i nie była równoległa do żadnej
z pozostałych pięciu płaszczyzn. Podaj maksymalną liczbę części, na które płaszczyzny
te mogły podzielić przestrzeń. | Zadanie 17
17 - Jaką najwikszą liczbę osi symetrii może mieć figura przestrzenna złożona z
trzech różnych prostych, z których żadne dwie nie są równoległe. | Zadanie 18
18 - W ośmiokącie P1 P2 P3 P4
P5 P6 P7 P8 wpisanym w koło, czworokąt
P1 P3 P5 P7 jest kwadratem o polu 5, a czworokąt
P2 P4 P6 P8 jest prostokątem o polu 4.
Jakie największe pole może mieć rozważany ośmiokąt ? | |