Zadanie 1
1 - Adaś i Tomek spędzili razem wakacje i każdego dnia przed południem
oraz po południu pisali w notesie literę S lub P w zależności od tego czy dana część
dnia była słoneczna, czy pochmurna. W tym okresie napisali 30 razy literę S i 16 razy
literę P. Przez 10 dni słońce świeciło od rana do wieczora. Ile chłopcy ci mieli
takich dni, w których chmury przesłaniały niebo przez cały dzień? | Zadanie 2
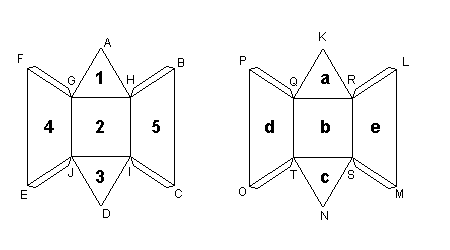
2 - Na rysunku przedstawiono siatki dwóch jednakowych pudełek tekturowych
o pięciu ścianach. Po sklejeniu tych siatek można otrzymane pudełka tak połączyć, aby
otrzymać piramidę (czworościan). Które ściany tych pudełek trzeba skleić? Podaj
pary wierzchołków tych ścian, które połączą się przy tym sklejeniu.
| Zadanie 3
3 - Pradziadek Janka jest w bardzo zaawansowanym wieku, ale nie ma jeszcze
stu lat. W ubiegłym roku jego wiek był liczbą całkowitą podzielną przez 8, a w przyszłum roku
będzie liczbą podzielną przez 7. Ile ma lat obecnie? | Zadanie 4
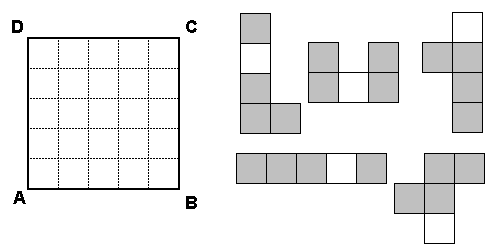
4 - Kasia ma 5 dziwacznych kafelków - pentamino pokazanych na
rysunku poniżej. Każdy kafelek złożony jest z 5 jednakowych kwadratów, z których jeden
jest biały. Kasia układając kadelki (bez odwracania) pokryła nimi kwadrat ABCD w taki
sposób, że białe kwadraty kafelków utworzyły układ symetryczny względem przekątnej BD
tego kwadratu. Podaj, na rysunku, wszystkie możliwe pokrycia kwadratu ABCD
spełniające podane warunki.
| Zadanie 5
5 - Zespół uczniów klasy V w drużynowym konkursie "WIEMY WSZYSTKO" otrzymał
w nagrodę 17 jednakowych długopisów, 38 jednakowych zeszytów i pudełko zawierające 73
cukierki czekoladowe. Próba sprawiedliwego podziału tych nagród okazała się niemożliwa, gdyż
liczby długopisów, zeszytów i cukierków nie dzieliły się bez reszty przez liczbę uczniów
zespołu. Marek zauważył, że w pozostałych częściach nagród, kłopotliwych do podziału, jest
tyle samo długopisów ile zeszytów i tyle, ile cukierków. Jak liczny był zespół
uczniów startujących w konkursie? | Zadanie 6
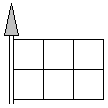
6 - Prostokątny proporczyk podzielony na 6 jednakowych kwadratów ma być
tak pokolorowany, aby jeden z tych kwadratów był niebieski, 2 - białe i 3 - czerwone.
Ile jest różnych sposobów pokolorowania proporczyka?
| Zadanie 7
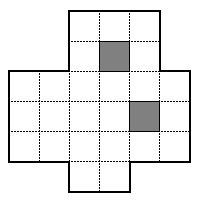
7 - Na parceli, pokazanej na rysunku, są dwa stawy. Teren parceli, bez
stawów, należy podzielić na cztery części złożone z całych kwadratów, dające się nałożyć
na siebie. Linie podziału zaznaczyć na rysunku pogrubionymi kreskami.
| Zadanie 8
8 - Mamy 11 monet ułożonych w jednym rzędzie tak, że mają one odkryte reszki.
W kolejnych ruchach możemy odwracać dokładnie trzy monety, leżące obok siebie, dowolnie wybrane.
Monet nie możemy przestawiać. Jak możliwie najmniejszą liczbą ruchów uzyskać układ,
w którym każde dwie monety leżące obok siebie mają odkrytą inną stronę, np. reszka, orzeł,
reszka, orzeł, ...? Podać układ końcowy i liczbę ruchów. | |
Zadanie 9
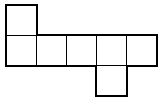
9 - Z sześciu jednakowych segmentów (rysunek poniżej) układamy zamknięty
łancuch w taki sposób, że dwa sąsiednie segmenty stykają się co najmniej jednym całym bokiem
małego kwadratu. Segmenty można odwracać. Ułożyć ten łańcuch tak, aby ograniczał on figurę o
możliwie największym polu. Podać pole tej figury w cm2 przyjmując, że
każdy kwadrat segmentu ma pole 1 cm2.
| Zadanie 10
10 - Dominika zbudowała ciąg liczb, pisząc na pierwszym miejscu najmniejszą
liczbę naturalną o sumie cyfr równej 1, na drugim miejscu najmniejszą liczbę naturalną o
sumie cyfr równej 2, itd..., na k-tym miejscu napisała najmniejszą liczbę naturalną, która
ma sumę cyfr równą k. Pierwszymi wyrazami tego ciągu są liczby: 1, 2, 3, ..., 9, 19, 29, ... .
Następnie wykreśliła z tego ciągu wszystkie te liczby, które nie są kwadratami liczb
naturalnych. Z początkowych wyrazów tego ciągu pozostawiła więc liczby: 1, 4, 9.
Ile jest wszystkich liczb, które nie zostały wykreślone? | Zadanie 11
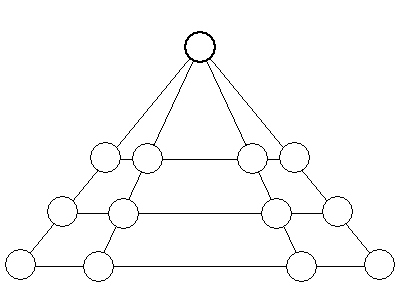
11 - W kółka piramidy należy wpisać liczby całkowite od 1 do 13 w taki sposób,
aby sumy liczb wpisanych w cztery kółka leżące na dowolnej, wspólnej prostej (poziomej lub
ukośnej) były równe. W odpowiedzi podać tylko liczbę wpisana w kółko umieszczone w
wierzchołku piramidy. Jeżeli uważamy, że zadanie nie ma rozwiązania, to w odpowiedzi
wpisujemy 0.
| Zadanie 12
12 - Prostokątną tablicę podzielono liniami równoległymi do boków na 120
pól kwadratowych. Beata, czarnym kolorem, wpisuje w pola tablicy kolejne liczby naturalne
od 1 do 120; rozpoczyna od pola w górnym lewym rogu i wypełnia kolejne wiersze od lewej
strony do prawej. Daniel, czerwonym kolorem, wpisuje obok kolejne liczby naturalne od 1
do 120; rozpoczyna z tego samego pola, ale wypełnia kolumny z góry na dół. Po wypełnieniu
tablicy zauważyli, że oprócz pola w górnym lewym rogu i pola w prawym dolnym rogu są
jeszcze inne pola, w których liczby wpisane kolorem czarnym i czerwonym są jednakowe.
Ile jest wszystkich takich pól w tej tablicy, łącznie z dwoma wymienionymi
wyżej? | Zadanie 13
13 - Punkt O jest wspólnym środkiem okręgów C1 i C2
o promieniach R1 = 10 cm i R2 = 5 cm, a punkt P leży na okręgu
C2. Punkt Q został wybrany na okręgu C1 w taki sposób, aby kąt OQP
był możliwie największy. Podać w stopniach miarę kąta OQP. | Zadanie 14
14 - Rozważamy wszystkie proste przechodzące przez wierzchołek C trójkąta
równobocznego ABC i na te proste rzutujemy prostopadle bok AB tego trójkąta. Obliczyć
pole figury utworzonej z tych rzutów. Do obliczeń przyjąć |AB| = 10 cm, √3 = 1,732
oraz π = 3.1416 i wynik podać w cm2 po zaokrągleniu do najbliższej liczby całkowitej.
| Zadanie 15
15 - W trójkącie ABC bok AB ma długość 10 cm, a bok AC ma długość 26 cm.
Jaką długość powinien mieć bok BC, aby najmniejszy kąt trójkąta ABC był możliwie
największy? Wynik podać w milimetrach po zaokrągleniu, w razie potrzeby, do
najbliższego milimetra. | Zadanie 16
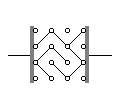
16 - Na izolacyjnej podstawce umieszczono dwie elektrody i 16 zacisków,
które można łączyć prętami metalowymi o długości równej przekątnej małego kwadratu
utworzonego z czterech zacisków (patrz rys.). Mamy 9 takich prętów jednakowej długości
i układamy je po jednym w każdym małym kwadracie wzdłuż dowolnie wybranej przekątnej
kwadratu. Przykład takiego ustawienia pokazany jest na rysunku. Ile jest różnych
ustawień 9 prętów, przy których nie popłynie prąd pomiędzy elektrodami A i B?
| |