Zadanie 1
1 - Liczby 2, 3, 4, 5 i 7 należy wpisać w puste kratki w takiej kolejności,
aby po wykonaniu zaznaczonych działań arytmetycznych otrzymać wynik możliwie największy.
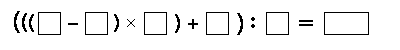
| Zadanie 2
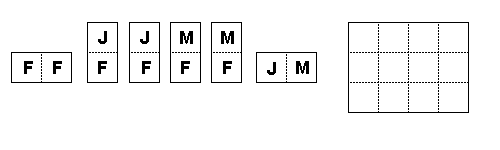
2 - Sześć kostek domino FFJM należy tak ułożyć na polach tablicy 3×4
(jedna kostka pokrywa dwa pola), aby w każdej linii poziomej tablicy występowały litery J
oraz M i dwukrotnie litera F, a do kładnie w jednej z tych linii pojawił się napis FFJM.
Kostek domino nie można obracać. W przypadku większej liczby rozwiązań podać jedno z nich.
| Zadanie 3
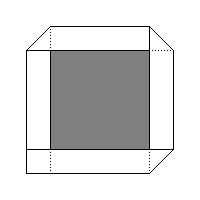
3 - Papierowy pasek o szerokości 1 cm zginamy pod kątem prostym w trzech
miejscach i następnie sklejamy dwa końce paska, które nakładają się na kwadrat 1 cm × 1 cm.
Pasek ten otacza zaciemniony kwadrat o polu 100 cm2.
Jaką długość miał ten pasek papieru ?
| Zadanie 4
4 - W każdej z klas Va i Vb było po kilkunastu uczniów (więcej niż 10, ale
mniej niż 20). Liczby uczniów w tych klasach były nieparzyste i różniły się o 4. Gdy klasy
te połączono w jedną klasę piątą, to okazało się, że liczba chłopców w tej połączonej klasie
była dwukrotnie większa od liczby dziewcząt. Ile dziewcząt było w tej połączonej klasie ? | Zadanie 5
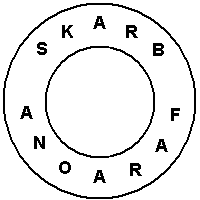
5 - Matylda i mateusz poszukujący skarbu FARAONA znajdują się przed drzwiami
do skarbca. Dzieci wiedzą, że drzwi te otworzą, gdy nacisną na jedną z liter napisu kołowego
"SKARB FARAONA" (jak na rysunku), ale nie znają tej litery. Wiedzą też, że naciśnięcie
niewłaściwej litery powoduje całkowite zablokowanie drzwi do skarbca. Nagle, pojawia się
dobroduszny staruszek i powiada do nich: "Wiem, że macie uczciwe zamiary i dlatego wyjawię
wam sekret, który pomoże odszukać właściwą literę. Należy rozpocząć od pierwszej litery słowa
SKARB i przechodzić do nstępnych liter według następującej reguły:
- jeżeli jesteśmy na spółgłosce, to przesuwamy się o 3 litery w kierunku zgodnym z ruchem
wskazówek zegara
- jeżeli natrafimy na samogłoskę, to musimy cofnąć się o 2 litery.
Jeżeli, rozpoczynając od litery S jako pierwszej, będziemy notować kolejne litery na które
będziemy trafiać stosując się do podanej reguły, to 1998-ma litera pozwoli wam otworzyć drzwi
do skarbca". Po tych słowach staruszek znika, a dzieci numerując kolejne litery S, R, A, B, ...
szybko znalazły właściwą literę. Podaj tę literę.
| Zadanie 6
6 - Kwadratowa plansza (5×5) podzielona jest na 25 pól kwadratowych
takiej samej wielkości jak ściany sześciennej kostki do gry. Kostkę kładziemy na polu w lewym
dolnym rogu planszy i toczymy do położenia w prawym górnym rogu planszy. Każdy ruch kostki,
po którym przetacza się ona z danego pola na pole sąsiednie polega na obrocie kostki o 90°
dookoła krawędzi pokrywającej się ze wspólnym bokiem sąsiadujących pól. Takie ruchy możemy
wykonywać tylko w prawo lub w górę planszy. W każdym z 9 położeń kostki na polach planszy
odczytujemy i dodajemy do siebie liczby oczek widoczne na górnej ścianie kostki.
Jaką największą sumę możemy uzyskać ? Przypominamy, że w typowej kostce do
gry sumy oczek na ścianach przeciwległych są równe 7. | Zadanie 7
7 - Kostki domino mogą służyć do oznaczania niektórych liczb jedno- i dwucyfrowych.
Na przykład kostka  oznacza liczbę 43, kostka
 liczbę 5, a kostka
 liczbę 50. Mamy kompletny zestaw 28 kostek domino
w którym występują wszystkie pary oczek utworzonych z liczb od 0 do 6. Przy pomocy czterech z nich
chcemy zapisać mnożenie
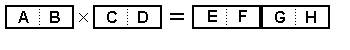
w którym liczba czterocyfrowa EFGH jest największa z możliwych. Napisz otrzymaną liczbę
EFGH cyframi. | Zadanie 8
8 - Mamy trzy jednakowe papierowe trójkąty prostokątne nierównoramienne.
Jeżeli jeden z nich przetniemy wzdłuż wysokości h wychodzącej z wierzchołka kąta prostego,
to będziemy mieli 4 trójkąty prostokątne podobne, z których dwa będą nadal jednakowe. Taką
operację przecinania możemy powtarzać wybierając jeden z posiadanych trójkątów prostokątnych
i przecinając go wzdłuż wysokości wychodzącej z wierzchołka kąta prostego. Po jakiej,
najmniejszej liczbie operacji przecinania otrzymamy zestaw trójkątów, w którym każde dwa mają
różne pola ?
| |
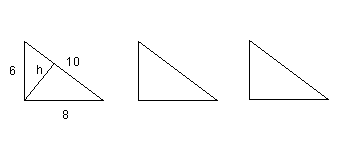
Zadanie 9
9 - Książka, którą czyta Bartek ma 200 stron. Drugi rozdział tej książki
rozpoczyna się na początku pewnej strony, a ostatnie zdanie tego rozdziału jest na końcu
innej strony. Bartek zauważył ze zdziwieniem, że jeśli doda cyfry numerów dwóch pierwszych
stron drugiego rozdziału, to otrzyma liczbę 18 i taką samą liczbę otrzyma gdy doda cyfry
numerów dwóch ostatnich stron tego rozdziału.
Ile stron ma drugi rozdział książki Bartka ? | Zadanie 10
10 - W czworokącie wypukłym ABCD o polu 100 cm2 środki boków AB, BC,
CD i DA oznaczono literami P, Q, R i S. Wewnątrz trójkąta APS wybrano punkt M, a punkty symetryczne
do punktów P, Q, R i S względem M oznaczono przez P1, Q1, R1 i
odpowiednio S1. Obliczyć pole czworokąta
P1Q1R1S1. | Zadanie 11
11 - Zosia napisała liczbę dwucyfrową, pomnożyła tę liczbę przez iloczyn jej
cyfr i otrzymała wynik 192. Janek niezależnie od Zosi napisał liczbę dwucyfrową większą od
liczby Zosi, a gdy pomnożył swoją liczbę przez iloczyn cyfr tej liczby, to otrzymał taki sam
wynik jak Zosia. Jaką liczbę napisał Janek ? | Zadanie 12
12 - Znaleźć największą liczbę naturalną n, dla której układ nierówności:
1≤x≤2, 2≤x2≤4, ..., n≤xn≤2n ma rozwiązanie i dla
otrzymanej liczby n podać najmniejszy i największy element w zbiorze wszystkich liczb x
spełniających te nierówności. | Zadanie 13
13 - Ogrodnik ma działkę w kształcie trapezu, w którym długości wszystkich boków
są liczbami całkowitymi metrów, a pole jest również liczbą całkowitą m2. Dłuższa
podstawa tego trapezu ma długość 70 m, a dwa boki nierównoległe do podstawy mierzą odpowiednio
104 m i 50 m. Jaką długość ma krótsza podstawa tego trapezu ? | Zadanie 14
14 - Na dowolnie wybranych polach pokratkowanej nieskończonej płaszczyzny
ustawiamy 61 pionów, przy czym na danym polu nie może znaleźć się więcej niż 1 pion. Dla
każdego ustawienia 61 pionów znajdujemy najmniejszą liczbę n o własności, że jeśli z tego
ustawienia usuniemy n odpowiednio wybranych pionów, to pozostałe będą na leżały na polach,
które nie mają wspólnych wierzchołków. Znaleźć największą z tych wszystkich liczb n. | Zadanie 15
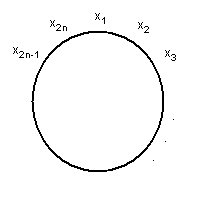
15 - Liczby naturalne 1, 2, 3, ..., 2n ustawiamy na okręgu w porządku x1, x2, x3, ..., x2n (jak na rysunku) w taki sposób, aby bezwzględna wartość różnicy każdej pary sąsiednich liczb była równa albo 2, albo 3. Podać, dla jakich parzystych liczb 2n takie ustawienie jest możliwe i wyznaczyć dla tych liczb najmniejszą możliwą wartość funkcji
S2n(x1, x2, ..., x2n) = | x1 - x2 | + | x2 - x3 | + ... + | x2n - x1 |.
| Zadanie 16
16 - W okrąg o średnicy D = 25/4 cm wpisujemy wszystkie trójkąty o bokach
całkowitoliczbowych (w centymetrach) i obliczamy pola tych trójkątów. Podać najmniejszą
i największą z otrzymanych liczb. | |