Zadanie 1
1 - Pieczątka (współczynnik 1)
Jaką datę odbije ta pieczątka?
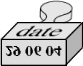
| Zadanie 2
2 - Konfitury (współczynnik 2)
Moja babcia przygotowała trzy rodzaje konfitur: truskawkowe, wiśniowe i morelowe. Są trzy słoje: jeden duży, jeden średni i jeden mały. W dużym słoju nie ma konfitur morelowych, a w małym nie ma wiśniowych. Konfitur truskawkowych jest więcej niż wiśniowych. Przyporządkuj każdy słój do konfitur, które on zawiera.
| Zadanie 3
3 - Farba (współczynnik 3)
Maxime chce pomalować swój pokój na kolor morelowy. Zrobił pierwszą próbę mieszając jeden litr farby białej, pół litra farby żółtej i jedną czwartą litra farby czerwonej. Kolor mu się podoba i postanawia przygotować wiecej farby. Do nowej porcji farby używa dwóch litrów farby zółtej. Jakie ilości farb czerwonej i białej musi dodać, żeby otrzymać taki sam kolor morelowy?
| Zadanie 4
4 - Podawanie w 6 (współczynnik 4)
Sześciu uczniów tworzy kółko i podają jeden do drugiego piłkę. W tej grze trzeba wykonać maksymalną liczbę podawań. Każde dziecko może podać piłkę do każdego ze swoich kolegów tylko jeden raz. Gra kończy się gdy uczeń, który ma piłkę nie może już wykonać podania (podał on już piłkę do wszystkich innych). Ile podawań maksymalnie można wykonać w tej grze?
| Zadanie 5
5 - Czarne pola (współczynnik 5)
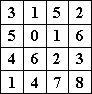
Zaczernić 3 pola w taki sposób, żeby suma liczb napisanych w każdym wierszu i w każdej kolumnie byla ściśle mniejsza od 13. Uwaga: nie można zaczernić dwóch pól, które mają wspólny bok.
| Zadanie 6
6 - Fibonacci w szkole (współczynnik 6)
Mały Fibonacci proponuje swojej nauczycielce nową grę rachunkową. Każdy z dwudziestu uczniów podaje po kolei jedną liczbę:
- Pierwszy mówi: "1"
- Drugi mówi: "1"
- Trzeci mówi: "2"
Następnie pozostali kontynuują mówiąc "3, 5, 8, 13, 21, ..." i tak dalej, a więc począwszy od trzeciego, każdy podaje liczbę będącą sumą dwóch poprzednich liczb. Jaką liczbę poda ostatni uczeń ?
| Zadanie 7
7 - Promień lasera (współczynnik 7)
Chcemy odchylić promień lasera używając zwierciadeł tego typu:
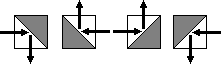
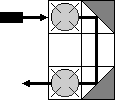
Promień lasera przechodząc przez baloniki niszczy je (przykład poniżej). Umieścić dokładnie 6 zwierciadeł według twojego wyboru na kratkowanej planszy 8 × 8 tak, aby zniszczyć wszystkie baloniki.

| Zadanie 8
8 - Odejmowanie (współczynnik 8)
Odnaleźć cyfry, które pozwalają wykonać odejmowanie przedstawione poniżej. Każdy symbol przedstawia inną cyfrę różną od zera. Uwaga: ma być spełniony warunek 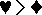

| Zadanie 9
9 - Plakat FFJM (współczynnik 9)
Francuska Federacja Gier Matematycznych (FFJM) zamówiła plakat ze swoim logo. Na rysunku proporcje nie są uwzględnione, ale dwa wskazane wymiary, wyrażone w centymetrach, są dokładne. Jaki jest obwód rombu centralnego? Podać odpowiedź w cm, zaokrąglając ewentualnie wynik do najbliższego cm.

| |
Zadanie 10
10 - Kura - rachmistrz (współczynnik 10)
Kura umie liczyć. Ustawiamy kurę przed stosem złożonym z 2004 jaj. Jest ona dobrze zorganizowana: zlicza jaja i ze zliczonych jaj tworzy obok drugi stos. Ale po każdych czterech zliczonych jajach znosi ona jedno jajo, które umieszcza w stosie jaj jeszcze nie przeliczonych. W końcu pozostał jej tylko jeden stos. Ile policzyła jaj?
| Zadanie 11
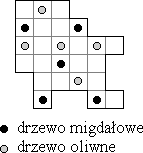
11 - Migdałowce i drzewa oliwne (współczynnik 11)
Stary José jest dumny ze swojej działki obsadzonej pięcioma drzewami oliwnymi i pięcioma migdałowcami. Czując swój rychły koniec chce on przekazać każdemu ze swoich pięciu synów część swojej działki. Każdy z nich będzie miał parcelę o tej samej powierzchni i tej samej formy zawierającą jeden migdałowiec i jedno drzewo oliwne. Narysujcie ten podział. Uwaga: Parcele na planie można odwracać.
| Zadanie 12
12 - Osiemnaste mistrzostwa (współczynnik 12)
Jak w każdym kryptarytmie, dwie różne litery przedstawiają zawsze dwie różne cyfry, a dwie różne cyfry są zawsze przedstawione przez dwie różne litery. Ponadto żadna liczba nie zaczyna się zerem.
DIX + HUIT + 1111 × ZERO = DIXHUIT
Znaleźć możliwie najmniejszą wartość DIXHUIT.
| Zadanie 13
13 - Nieostrożność (współczynnik 13)
Młody Malik wykonał na komputerze mnożenie dwóch liczb całkowitych. Chcąc uwidocznić swój wynik tłustą czcionką myli się i naciska klawisz operacji "sortuj". Operacja ta ustawia w kolejności rosnącej cyfry wszystkich wyświetlonych liczb. Malik widzi pojawiające się liczby napisane poniżej:
- Mnożna: 0246
- Mnożnik: 1457
- Iloczyn: 11338899
Pomóżcie mu odnaleźć prawidłowy iloczyn.
| Zadanie 14
14 - Kalkulator roku (współczynnik 14)
Ten kalkulator potrafi wykonywać tylko jedno działanie: mnożenie dwóch liczb. Nie jest możliwe wprowadzenie do niego liczby za pomocą klawiatury. Jedynymi liczbami, które może on używac są te znajdujące się w jego pamięci i zachowuje on systematycznie w pamięci wyniki wszystkich wykonywanych obliczeń. Można przywołać w każdej chwili dowolną liczbę znajdującą się w jego pamięci. Na starcie miał w pamięci tylko liczbę 2004. Jaka jest minimalna liczba mnożeń, które musi on wykonać, aby obliczyć 20042004?
| Zadanie 15
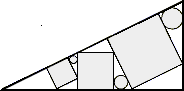
15 - Bardzo ściśnięte ustawienie (współczynnik 15)
Trzy kwadraty są zaklinowane w dużym trójkącie i trzy koła są wpisane w trójkąty (rys. poniżej). Promienie dwóch najmniejszych kół są, w centymetrach, równe 4 i 3√2. Obliczyć promień dużego koła. Przyjąć, w razie potrzeby, √2 = 1,414 i zaokrąglić ewentualnie wynik do 0,01 cm.
| Zadanie 16
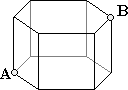
16 - Mrówka (współczynnik 16)
Bryła jest, stojącym na ziemi, graniastosłupem prostym o podstawie sześciokąta foremnego. Wysokość graniastosłupa i krawędź podstawy sa równe i mają po 10 cm. Mrówka znajduje się w punkcie A i chce udać się do punktu B po najkrótszej drodze. Jaką odległość przebędzie mrówka? Przyjąć, w razie potrzeby, √2 = 1,414 ; √3 = 1,732 ; √5 = 2,23 i zaokrąglić ewentualnie wynik do 0,01 cm.
| Zadanie 17
17 - Udana ucieczka (współczynnik 17)
Rysunek na lewo pokazuje 5 elementów ułożonych wewnątrz prostokąta 4 × 6. Szary pas jest pusty. Każdy z tych elementów można przemieszczać wewnątrz prostokąta suwając płasko tak, aby nie zachodził na inny element, a w przypadku, gdy zestawiamy ruchy w sposób ciągły, przesunięcie jednego elementu liczy się jako jedno wsunięcie. W ilu wsunięciach, co najmniej, tetramino (element kwadratowy) może przejść z pozycji rysunku na lewo do tej z rysunku na prawo?
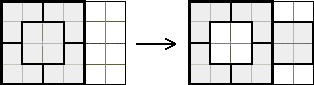
| Zadanie 18
18 - Płonna nadzieja (współczynnik 18)
Robinson właśnie przeżył zatonięcie statku. Siedzi on na beczce i czeka na ratunek. Widzi pojawający się na horyzoncie samolot relacji Paryż - Miami, a po 15 minutach stwierdza jego zniknięcie. Niestety, nie został on zauważony przez pilota. Robinson widzi odcinek łączący punkt ukazania się i punkt zniknięcia samolotu pod kątem 120°. Samolot ma stały kierunek lotu i leci na stałej wysokości 5000 m. Jaka jest prędkość samolotu w km/godz zaokrąglona do najbliższej dziesiątki? Nota: Promień kuli ziemskiej wynosi 6400 km. Przyjąć, w razie potrzeby, √2 = 1,414 ; √3 = 1,732 ; √5 = 2,23.
| |