1. BRAKUJĄCE LICZBY W każdym rzędzie znaleźć brakujące liczby
4 13 22 31 ? ?
18 ? 24 27 ? 33
| 
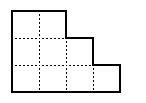
2. PODZIAŁ Podziel ten placek na trzy równe części tak, aby wszystkie trzy
mialy ten sam ksztalt.
| 
3. ROCZNICA MOICH URODZIN Urodziłem się 13 czerwca. Moja koleżanka Peggy urodziła
się 7 maja. W tym roku miała ona rocznicę urodzin w środe. Znajdź dzień mojej rocznicy
urodzin. | 
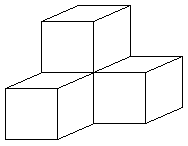
4. ZLĄCZONE SZEŚCIANY Cztery małe sześciany sklejono w sposób pokazany na
rysunku. Alexis kładzie tę bryłę na dłoni i liczy wszystkie ściany małych sześcianów, które
może zobaczyć. Ile ich policzy ?
| 
5. TRÓJKOLOROWANIE Na tej trójkątnej kracie trzeba pokolorować pewne trójkąty
przestrzegając następujących reguł:
- nie można kolorować trójkąta z liczbą
- liczba wpisana w trójkąt wskazuje ile sąsiednich trójkątów należy pokolorować.
Przykład:
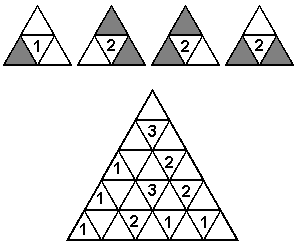
| 
6. WIWAT NOWOŻEŃCY Claudie oprawiła swoje zdjęcie ślubne (prostokąt o
długosci 17 cm i szerokości 8 cm) używając drewnianej listwy do ram. Ramka ma szerokość
2cm. Dla Claudie zostaje tylko osiem trójkątnych drewnianych ścinków. Podaj
długość kawałka listwy, który ona kupiła, aby sporządzić ramkę.

| 
7 . W POSZUKIWANIU ZAGINIONYCH SYMBOLI Oto siatka sześcianu, na każdej
ścianie którego znajduje się symbol. Sześcian ten jest przedstawiony kilkakrotnie na rysunku,
ale pewne symbole zmazano. Znajdź brakujące symbole.
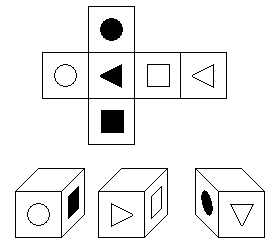
| 
8. PORWANIE PREZYDENTA Porwano prezydenta FFJM. Policja ma trzech podejrzanych:
dwóch, którzy zawsze kłamią i jednego, który zawsze mówi prawdę. Oto wyciąg z przesłuchania:
- Nicolas: "Nie porwałem prezydenta".
- Mathieu: "Nicolas nie jest kłamcą".
- Marie: "Mathieu nie porwał prezydenta".
Kto porwał prezydenta ? | 
9. RÓWNOŚĆ DO USTALENIA Thomas zadaje sobie pytanie, czy 6×6 może być
równe 9×4. Nina, jego siostra, pokazuje mu wtedy kwadrat 6x6, który podzieliła na 9 kawałków.
"Spróbuj pokryć prostokąt 9×4 tymi dziewięcioma kawałkami tak, żeby nie zachodziły na siebie,
a to ustali twoją równość. Jest to możliwe nawet bez odwracania żadnego z tych kawałków, a żeby ci
pomóc, dwa z nich już umieściłam w prostokącie. Narysujcie siedem pozostałych kawałków w
prostokącie.
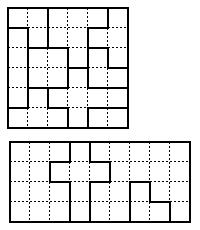
| |

10. ZYGZAKI KONIKA SZACHOWEGO Konik szachowy przemieszcza się po dużej szachownicy
składającej się z 20×20 pól. Przypominamy, że konik szachowy przemieszcza się po przekątnej
prostokąta 2×3 (uważamy, że konik ustawia się zawsze w środku pola). Po przebytej, zgodnie
z regułą przemieszczania się, zygzakowatej trasie, konik wrócił na swoje pole wyjściowe.
Ile co najmniej wykonał skoków? | 
11. PRZYGOTOWANIE BANKIETU Mathilde i Mathias zaprosili swoje rodziny i
przyjaciół na przyjęcie urodzinowe. Mathias ustawia dwa duże prostokątne stoły i stwierdza
co następuje: "Jeżeli połączę te stoły pewnym bokiem, aby utworzyc jeden duży prostokąt,
to dookoła będzie mogło zasiąść tylko 20 zaproszonych osób (przewidując takie samo miejsce
dla każdego gościa). Jeżeli natomiast zestawię je innym bokiem, to zyskam 2 miejsca, ale
to jeszcze nie wystarczy". Mathilde zauwaza: "To prawda, możemy więc, w tej sytuacji zrobić
przyjęcie przy dwóch oddzielnych stołach zwlaszcza, że jest tyle samo dzieci co dorosłych i
wtedy wszyscy zasiądą". Ile dzieci będzie obecnych na tym przyjęciu ? | 
12. FIGURA DO POKRYCIA Mathias ma cztery prostokąty 2×1 i pięć kwadratów
1×1 i chce tymi dziewięcioma czworokątami pokryć całkowicie figurę pokazaną obok. Kiedy
położył jeden kwadrat 1×1 na jedno z pól tej figury Mathilde zwróciła mu uwagę, że po
takim pierwszym ruchu nie bedzie mógł pokryć całej figury. Na jakim polu Mathias położył
swój kwadrat 1×1 ?
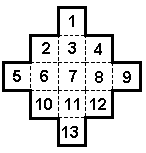
| 
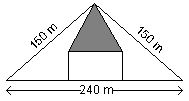
13. POLE PROFESORA PYTHALESA Profesor Pythales zostawił w spadku swoim czterem
synom teren w kształcie trójkąta równoramiennego o wymiarach 240m, 150m i 150m do równego podziału,
każdy z nich ma otrzymać parcelę o tej samej powierzchni co parcele jego braci. Ale najstarszy brat
domaga się parceli prostokątnej a najmłodszy - parceli w kształcie trójkąta równoramiennego.
Ostatecznie zgadzają się na podział przedstawiony na rysunku powyżej. Jaki jest obwód
parceli najmłodszego z braci? (szary trójkąt).
| 
14. CAŁKIEM NOWY KOD FFJM zamyka odpowiedzi do swoich testów w kasie pancernej,
której drzwi można otworzyć tylko za pomocą numeru kodu. Kod ten uważany za liczbą calkowitą nie
kończy się zerem i ma nastepującą szczególną własność: Jeżeli wykreślamy pewną cyfrę, to otrzymana,
nowa liczba jest równa 1/9 liczby początkowej. Można
wtedy ponownie wykreślić jedną cyfrę tej drugiej liczby i otrzymać dokładnie
1/81 kodu początkowego. Jaki jest numer kodu
kasy pancernej FFJM ? | 
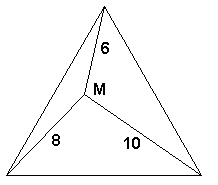
15. TRÓJKĄTNY LAS Mathias zabłądził w lesie, który ma kształt trójkąta
równobocznego. Nie zna on wymiarów lasu ale posługuje się specjalnym instrumentem i
sprytnym rachunkiem, może ustalić, że znajduje się o 6 km od jednego z wierzchołków tego
lasu, o 8 km od drugiego i o 10 km od trzeciego wierzchołka. Jaka jest
powierzchnia lasu ? Można przyjac, w razie potrzeby, że
√3≈1.7321 i zaokrąglić wynik do
0.01 km2.
| 
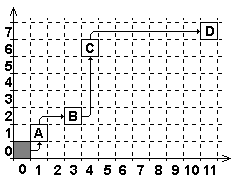
16. PRZEMIESZCZENIE NA SIATCE KWADRATOWEJ Kwadracik znajduje się w kratce (0;0).
Wykonuje się po kolei dwa nastepujące ruchy:
- przesunięcie o jedną kratkę na prawo z nastepującym po nim przesunięciem do góry
o liczbę kratek równą liczbie zaznaczonej na osi odciętych.
- przesunięcie o jedną kratkę do góry z nastepującym po nim przesunięciem na prawo
o liczbą kratek równą liczbie zaznaczonej na osi rzędnych.
Na rysunku pokazano przykładowo położenia A,B,C,D kwadracika po czterech pierwszych ruchach.
Jakie będą współrzędne Z ?
| 
17. SERWETKI FIBO Fibo ma serwetę w kształcie pięciokąta foremnego.
W pierwszym etapie usuwa, z każdego boku pięciokąta, trójkąt w taki sposób, aby otrzymać
6 mniejszych pięciokatów foremnych łączących się jednym bokiem (rysunek poniżej). W drugim
etapie stosuje tę operację "wycinania" do poprzednio otrzymanej figury i uzyskuje serwetkę
przedstawioną na rysunku dolnym. Po piątym etapie, Fibo otrzymuje serwetkę, której pole
wynosi 1 dm2. Jakie było pole powierzchni serwety wyjściowej wyrażone w
cm2 po zaokrągleniu do najbliższego cm2 ? ( 2,236 ≈ √5).

| 
18. STRAŻNIK - ARYTMETYK Roztargniony profesor został w Muzeum CNAM po
jego zamknięciu. Strażnik, który zauważył obecność profesora, zwrócił mu uwagę, że nie
wolno przebywać w muzeum poza godzinami otwarcia dla zwiedzających i zaproponował mu
wypuszczenie "na wolność" za rozwiązanie następującej zagadki: "Oto liczba: 3 892 153.
Maszyna kongruencyjna braci Carissan ustali panu migiem, że ta liczba jest równa 17522+9072,
ale także jest równa 11722+15872. Czy potrafiłby pan znaleźć dwie liczby całkowite większe od 1,
których jest ona iloczynem ?". Jakie to dwie liczby ? | |